Si recordamos un poco aquella serie de artículos técnicos sobre radar, recordaremos que las frecuencias que utilizábamos, los osciladores locales y las señales, eran todas ondas senoidales de una frecuencia determinada. (Si esto os suena a chino os recomiendo leer antes de seguir la saga de artículos dedicados a radar).
Sin embargo, ocurre que como todo en este mundo nada es perfecto y no iban a ser menos nuestros osciladores y señales de radar, que aunque muy próximos a la perfección, no son ondas senoidales perfectas ¿Y esto en que nos afecta? Nos afecta en interferencias, en problemas indeseables y en una falta de rendimiento del equipo.
Antes de presentaros a las espúreas, quiero comentar una serie de fenómenos físicos que nos ayudarán a entender este concepto.
SERIES DE FOURIER
Primero definiré lo que es una ONDA PERIODICA. Una onda periódica es aquella que se repite en el tiempo, por ello una onda senoidal es una onda periódica, pero también lo es una onda cuadrada, una rectangular o un diente de sierra por ejemplo.

Series de FOURIER: Este señor matemático que hace un porrón de años (y algunos siglos) y con nombre que me recuerda a una marca de fabricantes de cartas, postuló que una onda periódica se podía descomponer en la suma de infinitas ondas senoidales de frecuencia armónica (o sea, múltiplo de la frecuencia de la onda periódica).
Armónicos de una señal: Este postulado matemático luego ha sido comprobado físicamente viendo que, efectivamente, si cogíamos una onda periódica y le aplicábamos los correspondientes filtros, podríamos sacar estas “ondas senoidales” que componen la onda original.
Se define entonces como armónico a esta onda senoidal que es parte de la composición total de la onda periódica. Además esta onda “armónica” como a hemos dicho es múltiplo de la frecuencia de la onda periódica.
Sabiendo que múltiplo de la frecuencia es cada onda armónica, se definen los armónicos como:
• Primer armónico o frecuencia fundamental: El armónico con igual frecuencia que la onda periódica.
• Segundo armónico: El que tiene una frecuencia doble de la fundamental.
• Tercer armónico: El que tienen una frecuencia triple de la fundamental.
• Armónico enésimo: El que tienen una frecuencia enésima de la fundamental.
A veces, además de sumar un numero infinito ondas senoidales, es necesario también añadir una cantidad fija, un valor continuo, de ahí vienen el nombre de COMPONENTE CONTINUA de la señal. Es simplemente sumarle una señal continua a nuestro infinito número de ondas senoidales.
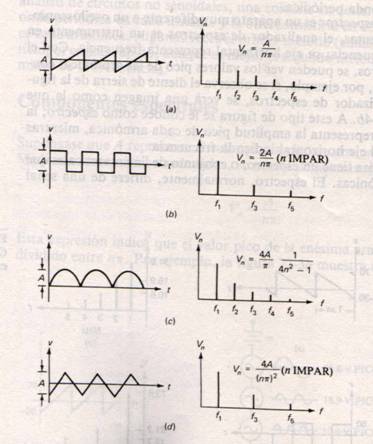
Espectros: Que nada tiene que ver con fantasmas ni con el Iker Jiménez. Los armónicos se pueden representar en una gráfica donde en un eje ponemos la amplitud (cual grande es el armónico) y en el otro eje ponemos las frecuencias. Esto es lo que denominamos “espectro” de la señal, una representación gráfica de los armónicos y la amplitud de los mismos. Viendo un espectro, un experto puede saber más o menos de que tipo de onda periódica se trata (si es una cuadrada, una triangular o un churroide).
Vemos que contra mayor es el armónico, menos es su amplitud. Por ello en la práctica no se utilizan infinitos armónicos para definir una señal, con 5 o 7 armónicos (o incluso a veces menos) la aproximación suele ser mas que suficiente.
Recapitulando, cualquier onda periódica se puede descomponer, o se puede generar, como la infinitas sumas de ondas senoidales de frecuencia múltiplo de la primera, y de amplitud variable con la suma (a veces) de una componente continua.
Onda periódica= Componente CC + 1er armónico + 2 armónico + ..+ enésimo armónico
A efectos prácticos solo se duelen utilizar hasta el 5 armónico, ya que el resto suelen ser tan pequeños en amplitud que son despreciables.
A continuación os pongo los espectros de 4 ondas periódicas muy utilizadas en electrónica.
DISTORSION ARMONICA O DE AMPLITUD
Como hemos dicho al principio del artículo, como los elementos no son ideales (amplificadores, antenas emisoras, etc) estos en vez de generar una onda senoidal pura, generan una onda que es “casi senoidal” pero que no lo es.
Imaginemos por ejemplo, un oscilador o un amplificador (recordad los artículos sobre radar), la onda senoidal obtenida, y luego amplificada por ejemplo para una frecuencia intermedia, no es una señal perfecta.
En el siguiente dibujo lo vemos (eso si, esta muy exagerado).

La diferencia existente entre la onda patrón, y la onda de salida, es lo que se denomina “distorsión de amplitud”. Entonces lo que tenemos no es una onda periódica senoidal para la frecuencia fundamental f, lo que tenemos es una onda periódica compuesta por una serie de ondas senoidales perfectas (los armónicos).
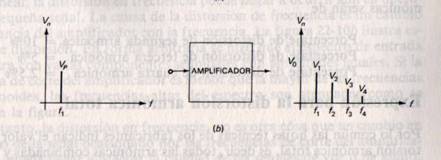
Evidentemente contra mejor sean los osciladores y amplificadores, mas perfecta será la onda senoidal obtenida y menor serán los armónicos de estas señales. Pero cuidado no hay que confundir estos armónicos con las señales suma y diferencia que obtenemos al mezclar frecuencias, es otra cosa.
Espúreas
Son aquellos armónicos indeseables que nos salen por la no linealidad (no perfección) de los equipos electrónicos. Hay que evitarlos ya que pueden provocar un mal funcionamiento en el equipo, o en equipos adyacentes.
¿Por qué son tan malas estas espúreas? Porque pueden afectar en circuitos del equipo y hacer que funcione mal ya que en teoría no deberían de existir señales de esas frecuencias (frecuencias armónicas), creo que con un ejemplo se verá mucho mas claro.
Imaginemos que tenemos un receptor heterodino tal y como hemos visto en nuestra serie de radar. Supongamos que tenemos cerca otro oscilador local que funciona mal y genera muchos armónicos indeseables, y que casualmente su frecuencia de trabajo sea una fracción entera de la frecuencia de nuestro oscilador, por ejemplo que su segundo armónico coincida con la frecuencia de nuestro oscilador.
Entonces aunque el oscilador adyacente funcione a una frecuencia que nada tiene que ver con nuestro oscilador heterodino, uno de sus armónicos coincide con esta frecuencia, y si tiene la amplitud suficiente (una gran distorsión) afectaría a nuestro receptor heterodino haciendo que funcione mal, traducido en pérdida de sensibilidad, ruido, interferencias… o simplemente, que no funcione.
La manera de eliminar los armónicos, si no somos capaces de generar un tratar una señal senoidal con la máxima pureza que requiere el equipo, es echar mano de los filtros. Si utilizamos un filtro pasa-bajos (recordemos aquel que solo deja pasar las frecuencias por debajo de un valor) resolveremos el problema de los armónicos, ya que los armónicos SIEMPRE van a tener una frecuencia superior a la frecuencia




















